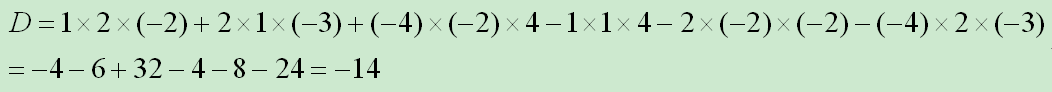二阶行列式

有如下二元线性方程组：

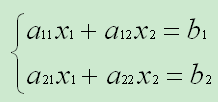
求解方程组可得：

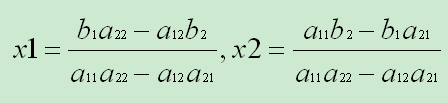
可以看到，两式中分子、分母都是四个数两两相乘再相减。其中分母 a₁₁a₂₂ - a₁₂a₂₁ 是由二元方程组的四个系数确定的，将这四个数排列如下 2 x 2 数表：

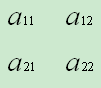
将 a₁₁a₂₂ - a₁₂a₂₁称为以上数表所确定的二阶行列式，记作：

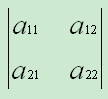
其中 a_ij (i = 1, 2 …, j = 1, 2 … ) 称为行列式的元素或元，i 为行标，j 为列标。

上面行列式也可以用对角线法则来记忆：

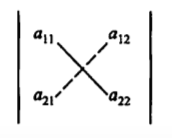
其中左上到右下的实线为主对角线，右上到左下的虚线为副对角线，二阶行列式即为主对角线之积减去副对角线之积。

假设另：

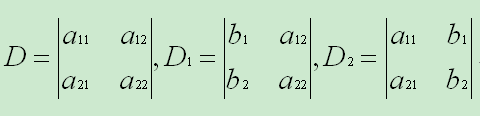
则上述二元方程组结果可记作：

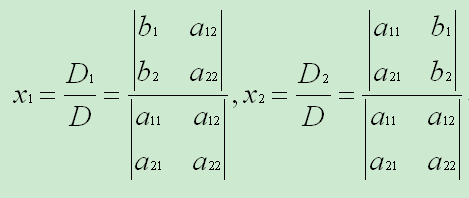
其中，D 是由二元方程组的系数所确定的二阶行列式（称为系数行列式），D₁ 是用 b₁、b₂ 替换 D 中 x₁ 的系数 a₁₁、a₂₁ 所得的二阶行列式，D₂ 是用 b₁、b₂ 替换 D 中 x₂ 的系数 a₁₂、a₂₂ 所得的二阶行列式。

我们可以使用上面的公式来解二元线性方程组。

例如方程组：

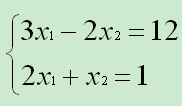
其中：

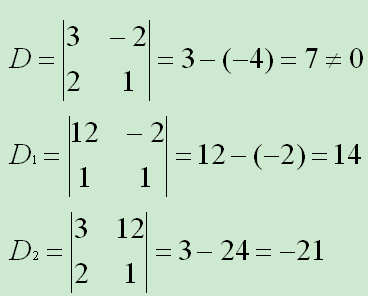
因此：

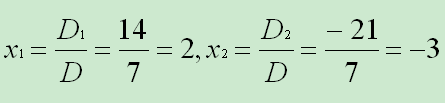
三阶行列式

如下为三阶行列式：

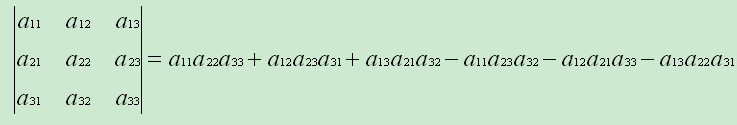
三阶行列式中包含6项，每项为不同行不同列的三个元素的乘积并冠以正负号，其规律遵循如下对角线法则：

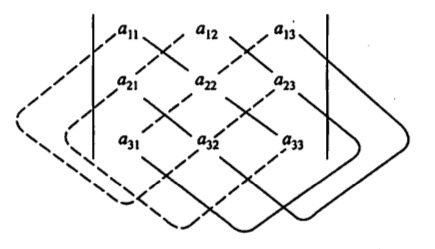
图中有三条平行与主对角线的实线联线，三条平行与副对角线的虚线联线；三阶行列式中实线上三元素乘积相加，减去虚线上三元素的乘积。

如下三阶行列式：

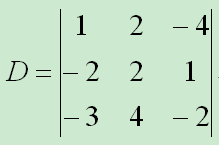
按照对角线法则可计算结果为：